[Papers] 3D Gaussian Splatting for Real-Time Radiance Field Rendering (SIGGRAPH 2023)

3D Gaussian Splatting for Real-Time Radiance Field Rendering

[Paper][Github][DEMO]

Title: 3D Gaussian Splatting for Real-Time Radiance Field Rendering
Journal name & Publication Date: SIGGRAPH 2023-08-08
First and Last Authors: Kerbl, Bernhard

About 3D Gaussian

논문을 들어가기전 Gaussian 및 3D Gaussian에 대한 기본적인 개념들을 복기하고 정리하는 부분.

Gaussian
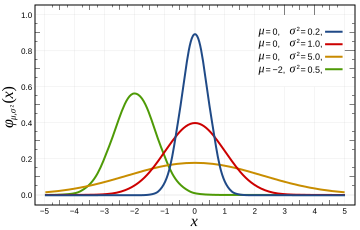
가우시안은 확률에서 정규분포의 확률 밀도 함수(PDF)를 나타낼 때 주로 사용되는 함수이다. 평균, 분산, 표준편차만으로 정의될 수 있다는 것이 특징이다.

\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

$\mu$: 평균
$\sigma^2$: 분산 (표준편차 $\sigma$의 제곱)
$x$: 확률 변수

특징: 평균을 중심으로 대칭적으로 분포하며, 분산이 클수록 데이터가 더 넓게 퍼지며 분포의 첨도(kurtosis)가 낮아진다.

공분산(Covariance)
공분산이란 두 개 이상의 변수 간의 상관 관계를 수량화하는 척도이다. 데이터의 분산이 한 변수에서 다른 변수로 어떻게 함께 변화하는지, 어떤 관계를 갖고 있는지를 나타낸다.

**공분산 행렬$\sum$(Covariance Matrix) **
공분산 행렬은 다변량 데이터(여러 변수)에서 각 변수 간 공분산을 행렬 형태로 나타낸 행렬이다.

\[\Sigma = \begin{bmatrix} \text{Var}(X_1) & \text{Cov}(X_1, X_2) & \cdots & \text{Cov}(X_1, X_n) \\ \text{Cov}(X_2, X_1) & \text{Var}(X_2) & \cdots & \text{Cov}(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \cdots & \text{Var}(X_n) \end{bmatrix}\]

$\text{Var}(X_i)$: 변수 $X_i$의 분산$(\sigma_i^2)$
$\text{Cov}(X_i,X_j)$: $X_i$와$X_j$ 간의 공분산

특징

대칭 행렬: $\text{Cov}(X_i,X_j) = \text{Cov}(X_j,X_i)$
대각 성분: 대각선 요소는 각 변수의 분산.

3D Gaussian

\[f(x,y,z)=\frac{1}{(2\pi)^{3/2}\left|\sum\right|^{1/2}}e^{-\frac{1}{2}r^\top\sum^{-1}r}\]

$r$ = $\left[x-\mu_x,y-\mu_y,z-\mu_z\right]^T$: 평균($\mu$)에서의 거리 벡터
$\sum$: 3x3 공분산 행렬 (크기와 방향성을 조정)

특징

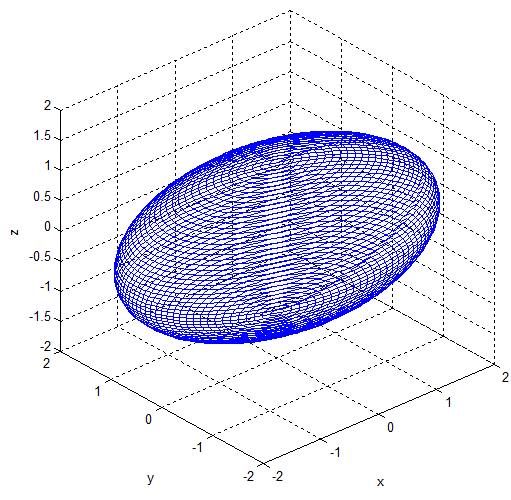
공간적 분포(위치): 3D 공간의 특정 지점(평균)을 중심으로 데이터가 퍼진다.
공분산 행렬(모양, 방향): 3D Gaussian의 분포 모양은 공분산 행렬 $\sum$에 의해 결정된다.
- 대각 성분(분산): 각 축의 분산을 통해 Gaussian의 장축, 단축 크기를 결정한다.
- 비대각 성분(공분산): 비대각의 공분산 값을 통해 축 사이의 회전을 나타낸다. 즉, 타원의 방향을 결정한다.

\[\Sigma = \begin{bmatrix} \sigma_x^2 & \sigma_{xy} & \sigma_{xz} \\ \sigma_{xy} & \sigma_y^2 & \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_z^2 \end{bmatrix}\]

질문

3D Gaussian은 함수형태로 point cloud를 표현하므로 implicit(암시)하게 정의되는것이 아닌가?
- 함수 형태로 표현되기 때문에 implicit한 것은 맞다. 하지만 Gaussian이라는 것도 결국 $\mu$와 $\sum$로 표현이 되기 때문에 굳이 말하자면 명시적으로 나열될 수 있는 표현이다.
- 결론적으로 implicit한 표현으로 보았을 때 Gaussian함수는 연속적인 표현이 가능하며 메모리 효율성을 챙기고 부드러운 분포를 보일 수 있다는 장점을 가지게 된다.
왜 공분산 행렬을 RSS^TR^T와 같이 정의하는것일까 ?
- Symmetric한 성질을 만들기 위하여.
- $(AA^\top)^\top = A^\top A$

radiance field

3D 공간에서 빛과 색상 분포를 의미하는 함수, 개념.

1. Abstract & Introduction

3D 장면 표현 방식에서는 그동안 많은 발전이 이루어져 왔다. 대표적으로 NeRF는 MLP를 사용하여 암묵적인 특징을 최적화(implicit optimization)하며, 높은 성능을 보여주고 관련 논문들이 지속적으로 등장하고 있는 중이다.

이 분야에서는 공통적으로 해결해야 할 문제와 도전 과제로 다음과 같은 점들이 존재한다.

여러 장의 사진을 통해 장면을 효율적이고 빠르게 최적화 하고 표현하는 것.

실시간 렌더링(real-time rendering) 을 가능하게 하는 것.

이번 논문에서는 기존의 SOTA 모델보다 더 빠르고 효율적인 최적화와 표현, 그리고 실시간 렌더링을 지원하는 3D Gaussian Splatting을 제안한다.

논문에서는 다음과 같은 3가지 주요 방법론을 통해 이를 실현한다.

비등방성 3D Gaussian의 도입 (Anisotropic 3D Gaussians)

high-quality radiance field를 비구조적으로 표현하기 위한 방식.

이르르 통해 장면의 세부 정보를 더 정확하게 표현이 가능하다.

3D Gaussian 속성 최적화 (Optimization Method of 3D Gaussian Properties)

3D Gaussian의 속성을 최적화.

adaptive density control을 교차적으로 활용

GPU 기반 빠른 미분 가능 렌더링 (Fast, Differentiable Rendering Approach for the GPU)

가시성 인식(visibility-aware): 시점에서 보이는 부분만 효율적으로 계산

비등방성 splatting(anisotropic splatting): 더 정밀한 장면 렌더링 가능

fast backpropagaton: 효율적인 학습과 novel view synthesis 지원

2. Related Work

3. Overview

Input
- 입력 데이터는 정적인 장면의 이미지 세트와 SfM(Structure-from-Motion)을 통해 보정된 카메라 정보가 들어온다.
3D Gaussian
- SfM을 통해 들어온 point cloud를 통해 3D Gaussian 집합을 생성한다.
- 3D Gaussian은 위치(mean), 모양과 방향(covariance matrix), 불투명도($\alpha$, opacity)를 통해 정의된다.
Radiance Field
- Radiance Field Color는 spherical harmonics, SH를 사용하여 표현된다.
Optimization
- 3D Gaussian의 주요 파라미터인 mean, covariance matrix, $\alpha$, SH coefficients를 최적화하여 randiance field를 올바르게 표현한다.
- 이 과정에서 adaptive Gaussian density control가 교차적으로(interleaved) 적용된다.
Tile-based rasterizer
- 타일기반의 3D에서 2D 이미지로의 변환은 다음과 같은 효율성과 기능을 가진다.
  - 가시성 순서를 고려한 빠른 정렬로 $\alpha$-blending 지원.
  - 빠른 backward pass 구현
  - 가우시안의 개수 제한 없이 그래디언트 계산 가능.

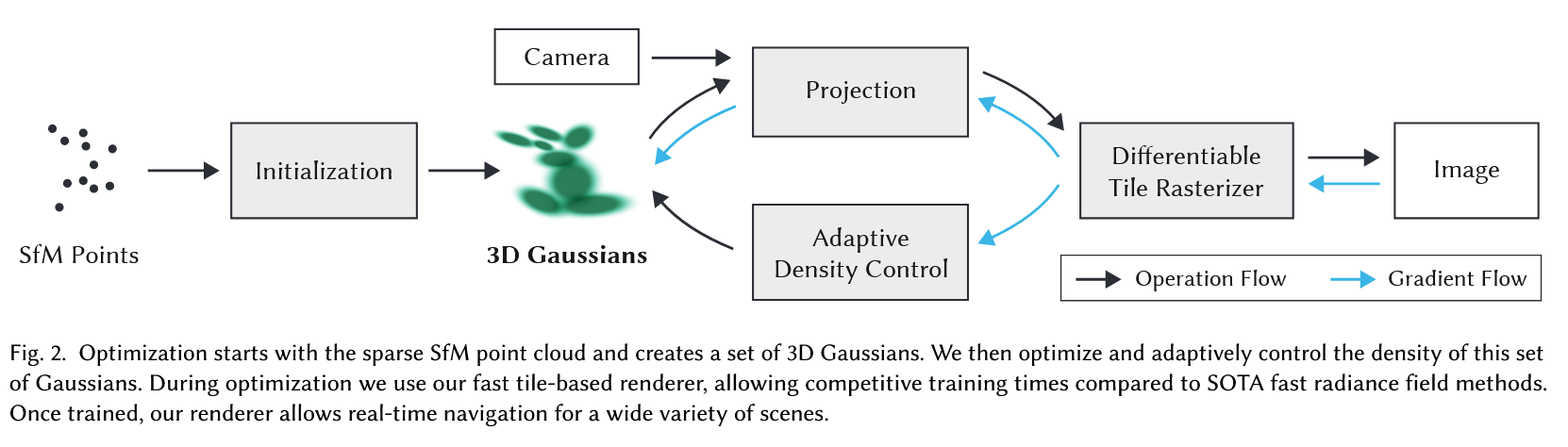
전체적인 procedure에 대한 도식화는 아래와 같다.

추가적으로 알아볼 것(SfM, spherical harmonic)

4. Differentiable 3D Gaussian Splatting

먼저 위에서의 한계점들을 극복하기 위해서는 미분가능한 volumetric 표현을 가지며 explicit한 특징으로 빠르게 렌더링이 가능한 표현법이 필요하다고 한다.
3D Gaussian은 미분가능한 표현법이며 2d splats로의 projection과 $\alpha$-blending을 통해 빠른 렌더링이 가능하기 때문에 선택했다고 한다.

3D Gaussian initialization
이전의 표현법들은 normal을 통해 추정하고 optimizing하는게 굉장히 challeging하다고 한다. 그래서 해당 논문에서는 normal정보가 필요없고 covariance matrix ($\sum$),centered point ($\mu$)를 통해 정의할 수 있는 3D Gaussian을 사용한다.

\[G(x) = e^{-\frac{1}{2}(x)^T\sum^{-1}(x)}\]

2D Projection Transform
위에서 표현한 3D Gaussian을 projection을 위해 2D camera 좌표계인 $\Sigma’$로 변환 할 필요가 있다.

\[\Sigma' = J W \Sigma W^T J^T\]

$W$: viewing transformation으로 카메라 좌표계로의 변환을 의미한다.
$J$: projective transformation인 Jacobian행렬로 비선형적인 투영변환을 통해 선형 근사하는 역할을 한다.
Why 이런 식이 나올까 ?

쉽게 말해 $\Sigma_{WJ} = \Sigma’$으로 볼 수 있는데 Covariance matrix $\Sigma$ Covariance matrix를 직접적으로 최적화 하기 위해서는 $\Sigma$가 positive semi-definite 조건을 가지고 있어야 한다. 만약 해당 조건을 충족하지 못하고 최적화를 시킨다면 잘못된 optimizing을 할 수도 있게 된다.

Positive semi-definite 이를 위해 scaling matrix $S$와 rotation matrix $R$을 사용하여 더 직관적이고 표현력이 높은 $\Sigma$를 구성하였다.

어떻게 이렇게 정의가 가능한 것인가 ?

이는 기존의 공분산이 가지는 의미를 통해 이해를 할 수 있다. 3D Gaussian에서 공분산은 타원체의 shape과 방향을 조정하는 역할을 하기 때문에 이는 Scale과 Rotation matrix만을 통해 표현이 가능하다는 것이다.
공분산의 대칭성 성질을 유지하기 위해 S와 R을 통해 표현할 때 전치행렬도 같이 곱해주어 공분산의 대칭행렬 성질을 그대로 유지하게 된다.

\[\Sigma = RSS^TR^T\]

5. Optimization with Adaptive Density Control of 3D Gaussians

Optimization

3D Gaussian Splatting의 최적화는 렌더링 결과와 훈련 데이터셋 이미지를 비교하며 반복적으로 수행한다. 이 과정에서 발생하는 3D-2D 투영의 모호성을 해결하고 효율적인 장면 표현을 만들어내기 위한 다양한 기법이 사용된다.
Optimization에는 geometry에서 생성, 제거, 이동하는 표현들이 가능해야 한다.

SGD
Optimizing 알고리즘으로는 GPU와 CUDA의 장점을 최대한 활용하기 위해 Stochastic Gradient Descent를 사용한다. 덕분에 빠른 rasterization이 가능했다고 한다.

Sigmoid
$\alpha$를 최적화하기 위해 sigmoid 함수를 사용하고 [0 - 1)로 제한하며 지수함수를 통해 공분산의 크기를 조절한다.

Inital & Loss
3D Gaussian의 각 축의 길이는 가장 가까운 세점까지의 평균 거리를 이용해서 초기화 해준다. 이를 통해 초반에 빠르고 안정적으로 수렴이 가능하다.
손실함수는 $\mathcal{L}_1$과 D-SSIM을 합친 함수로 구성되게 된다.

\[\mathcal{L} = (1-\lambda)\mathcal{L}_1 + \lambda\mathcal{L}_{\text{D-SSIM}}\]

D-SSIM이란 ?

D-SSIM은 Structural Similarity Index(SSIM)을 손실 함수로 사용할 수 있도록 미분 가능하게 변형한 버전이다.

D-SSIM은 렌더링된 이미지와 캡쳐된 훈련 뷰 간의 구조적 유사성을 비교하며 모델이 더 나은 3D 표현을 하도록 학습을 돕는다.

노이즈 제거, 초해상도, 스타일 전이 등의 구조적 차이?….

Adaptive Control of Gaussians

초반 SfM을 통해 얻은 sparse set에서부터 adaptively control을 통해 denser Gaussian으로 만들어 장면을 더 잘 표현하게 된다. 이후 100 iteration마다 밀도를 높이며 $\alpha(\text{transparent})$가 threshold보다 낮을 경우 제거하는 과정을 거친다.

Adaptive Control
Adpative Control에서 필요한 것은 빈 공간에 Gaussian을 통해 채워 넣는 것이다. 문제는 너무 적게 채워버리면 under-reconstruction 문제가 발생하고, 너무 큰 부분을 커버하면 over-reconstruction 문제가 발생한다는 것이다.

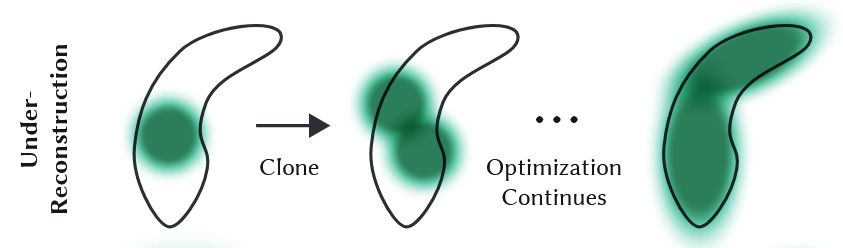
Under-Reconstruction
만약 해당 Gaussain에서 채워야 할 곳이 필요하다면 동일한 size를 가진 Gaussian을 복제하고 positinal gradient쪽으로 이동하여 빈공간을 채우게된다.

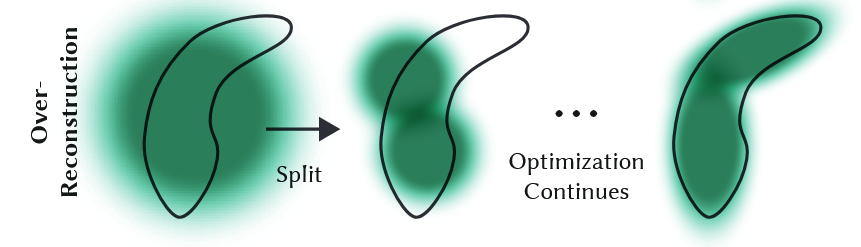
Over-Reconstruction
만약 너무 큰 Gaussian이라면 더 작은 Gaussian으로 나눌 필요가 있다. 이때는 실험적으로 얻은 $\phi$ = 1.6의 scale factor를 통해 작은 2개의 Gaussian으로 나누고 position을 이동하게된다.

Remove Gaussian
위에서 제시한 방법들을 토대로 Scene의 Gaussian을 최적화하면 Gaussian의 개수는 수도 없이 늘어난다. 이를 해결하기 위해 400 iteration마다 일정 threshold보다 낮은 $\alpha$값을 가진 Gaussian은 주기적으로 제거하는 방법을 사용한다.
결국 중요한, 유의미한 Gaussian들만 남게 되는 것이다.

6. Fast Differentiable Rasterizer for Gaussians

Goal
결론적으로 목표는 빠른 rendering과 빠른 $\alpha$-blending,최적화 구조를 개선하는 것으로 볼 수 있다.

Tile-Based Rasterizer
화면을 16x16 타일로 분할하여 병렬처리를 극대화한다. 각 타일은 독립적으로 처리되어 데이터 로드 및 계산 부분에서 효율화 한다. 99%의 Confidence에 해당하는 Gaussian만 유지하며 이 외의 Gaussain은 제거하여 계산의 불안정성을 방지한다.

$\alpha$-blending
타일 단위의 정렬을 기반으로 블렌딩을 수행한다. 추가적인 픽셀 단위 정렬 없이도 효율적으로 $\alpha$-blending이 가능하다. 픽셀의 불투명도가 1에 도달하면 해당 픽셀의 처리를 종료하며 각 타일 내 모든 픽셀이 포화되어도 종료하게 된다.

Backward Pass
Backward Pass 과정에서 Foward Pass의 Blending 정보를 활용하고 계산하여 효율성을 극대화한다.

차별점

픽셀 단위 정렬 제거: 성능을 크게 향상
제한 없는 기울기 계산: Gaussian 개수와 무관하게 처리 가능.
근사 $\alpha$-blending: 성능을 극대화하면서도 시각적으로 자연스러운 결과를 유지.

7. Implementation, Results and Evaluation

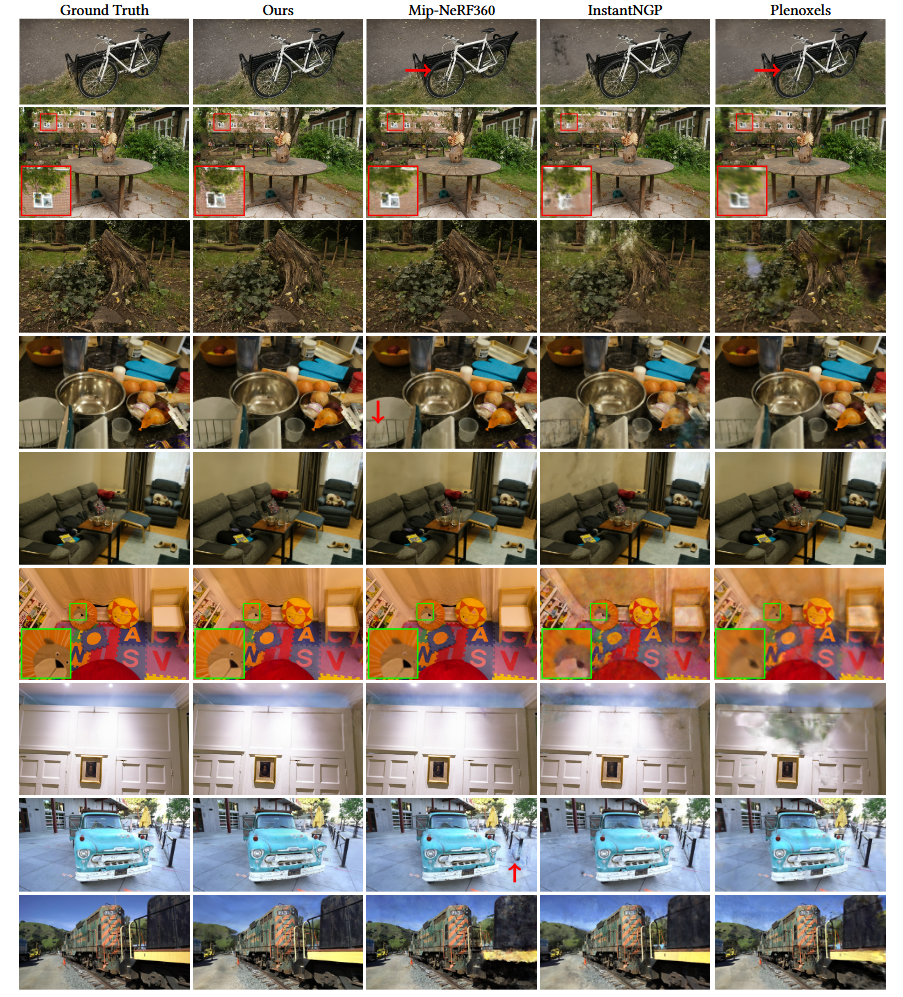
8. Discussion and Conclusions

Reference.

https://arxiv.org/abs/2308.04079
https://github.com/graphdeco-inria/gaussian-splatting
https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/
https://www.researchgate.net/figure/sualization-of-a-3D-Gaussian-model-a-Uncertainty-ellipsoid-for_fig5_231212225