[Papers] DETR: End-to-End Object Detection with Transformers (CVPR 2020)
End-to-End Object Detection with Transformers (CVPR 2020)
[Paper] [Github]
Title: End-to-End Object Detection with Transformers
Journal name & Publication year: Computer Vision and Pattern Recognition 2020
First and Last Authors: Nicolas Carion, Francisco Massa
First Affiliations: Facebook AI
저번주차 수업을 들으면서 중요하다고 판단되는 몇몇 논문중 한 논문으로 최대한 논문 원문을 보면서 이해해보려고 노력하며 정리해본다.
1. Abstract & Introduction
DETR은 Detection pipeline을 streamlines(간소화) 하며 hand-designed된 부분들을 최대한 제거하려고 노력했다고 한다. DETR의 큰 특징으로는 transformer의 encoder-decoder부분을 차용한 것과 predictions과 ground_truth의 bipartite matching(이분 매칭) loss를 적용한다는 것이다.
Object detection 분야에서의 목표는 boding boxes와 category labels 제공하는 것이다. DETR은 마지막 부분에서 prediction과 ground truth를 직접 비교하며 loss를 계산한다는 것인데, DETR은 (non-autoregressive)parallel decoding을 사용함으로써 병렬 처리 및 출력을 하며 출력된 bounding boxes를 각 ground truth의 짝지어진 box들과 매칭하고 bipartite matching loss를 이용하여 loss 계산을 한다고 한다.
Detection 분야에서 여러번 시험되고 많은 성능 개선이 된 Faster R-CNN과 performance적으로 비슷한 결과를 냈다고 한다. 큰 dataset에서는 더 좋은 성능을 주기도 했었지만 작은 dataset에서는 성능이 더 낮은 결과도 보였다고 한다.
DETR은 Detection 뿐만이 아니라 다른 더 복잡한 task 활용하여 좋은 성능을 뽑아냈다고 한다. 예를 들어 segmentation or pixel-level recognition 등등…
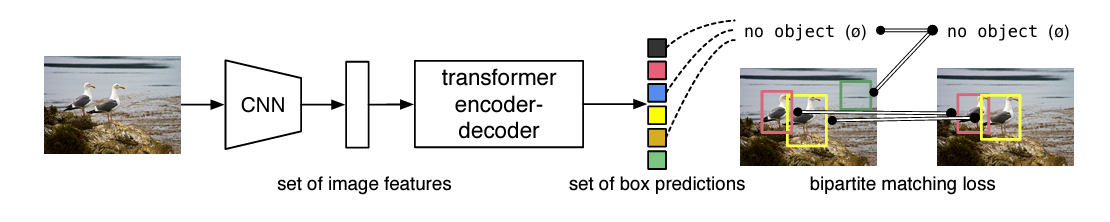
2. Related Work
2.1 Set Prediction
DETR에서는 set of box predictions를 위해 decoder구조에서 multi-task를 수행해야한다. 기존의 Detection model들에서 postprocessings + NMS(non-maximal suppression)가 수행하던 중복 bbox 제거가 set prediction에서의 걸림돌이다. direct set prediction에서 near-duplicates을 피하기 위해서 Hungarian algorithm을 기반으로 loss function을 설계한다고 한다. 이는 permutation-invariance(순열 불변성)을 적용하며 각 대상요소가 unique하게 일치하도록 해준다.
Hungarian Algorithm
match 해야할 두 vector $I$와 $J$가 존재할 때 I와 J에서 매칭되어 나온 cost를 최소화 또는 최대화 하는 이분 매칭 방법에 사용되는 알고리즘이다. 현재 Detection에서는 최대가 되는 cost를 원하는 것이니 최대 Hungarian Algorithm으로 예시를 들어본다.
-
먼저 행렬의 모든 값에서 최대가 되는 값(78)을 고르고 해당 값에서 각 원소들을 빼준다.
Track-1 Track-2 Track-3 Track-4 Detection-1 10 70 55 25 Detection-2 62 15 58 35 Detection-3 23 78 14 63 Detection-4 55 34 47 0 -
다음 Detection 행 기준으로 최솟값들에 대하여 행에서 값을 빼준다. (1 = 8, 2 = 16, 3 = 0, 4 = 23)
Track-1 Track-2 Track-3 Track-4 Detection-1 68 8 23 53 Detection-2 16 63 20 43 Detection-3 55 0 64 15 Detection-4 23 44 31 78 -
Track 열 기준으로 최솟값을에 대하여 해당 열에서 값을 빼준다. (1 = 0, 2 = 0, 3 = 4, 4 = 15)
Track-1 Track-2 Track-3 Track-4 Detection-1 60 0 15 45 Detection-2 0 47 4 27 Detection-3 55 0 64 15 Detection-4 0 21 8 55 -
그렇게 완성된 행렬을 확인해보았을 때 행렬에 있는 모든 0들을 vector의 개수에 맞게 덮을 수 있다면 최대 값을 구할 수 있게 된다. (ex. 0들을 열 기준으로 1,2,3,4를 선으로 덮을 수 있음.)
Track-1 Track-2 Track-3 Track-4 Detection-1 60 0 11 30 Detection-2 0 47 0 12 Detection-3 55 0 60 0 Detection-4 0 21 4 40 -
해당 0에 대한 값들을 matching을 시켜보면 (1,2) (2,3) (3,4) (4,1)의 값들이 되고 해당 값들을 모두 더하면 Hungarian Algorithm과 bipartite matching을 통한 최댓값을 구할 수 있게 된다. Final Assignment (Optimal Matching)
- Detection-1 to Track-2: 70
- Detection-2 to Track-3: 58
- Detection-3 to Track-1: 55
- Detection-4 to Track-4: 63 Maximum Total Value: 70 + 58 + 55 + 63 = 246
2.2 Transformers and Parallel Decoding
DETR에서 핵심적으로 중요한 부분이 Transformer 구조인데 Transformer는 처음에 NLP쪽에서 쓰이던 모델 구조였지만 memory 구조적으로나 long squences를 다루는 부분에서 기존의 RNN보다 낫다는 판단이었고 이를 Vision에서도 사용했었던 여러 논문을 토대로 Transformer 구조를 채택했다고 한다.
기존의 Transformer는 Sequence-to-Sequence구조로 출력이 하나씩 나오는 구조라 costly한 단점이 있었다. 이 부분을 해결하기 효율적으로 해결하기 위해 주어진 위치에서 객체의 위치와 클래스를 한꺼번에 예측하는 즉, 병렬적인 Decoding 문제로 변환하였다는 부분이 특징이다. 이는 기존의 Transformer대로 사용했을 때 순차적으로 예측하지 않고 병렬적으로 예측하여 inference 속도가 월등히 빨라지게 된다.
2.3 Object Detection
기존의 Detection 분야에서의 model들은 One-stage detector나 Two-staege detector나 모두 초반에 설정되는 추측 설정들에 따라 성능이 크게 좌우되는 경향이 있었다. 기존의 이런 불편함들을 모두 간소화시켜 end-to-end detection하는 방법을 보여준다. 기존의 Detection 마지막 부분에서 사용됐던 NMS 대신 direct set losses를 사용하여 이러한 post-processing 부분도 줄일 수 있었다.
3. The DETR model
3.1 Object detection set prediction loss
먼저 볼 부분은 set prediction loss로 해당 loss에서는 ground truth와 unique한 matching이 되어야 한다. 기본적으로 처음에 fixed-size로 지정된 N은 $\varnothing$(no object)로도 표현이 될 수 있기 때문에 이미지 내에서 detection 할 객체보다 더 많은 개수로 지정이 되어야 한다.
${\sigma \in S_N}$를 따라 N개의 예측값들을 permutation을 통해 $y_i$와 $\hat y_{\sigma(i)}$의 bipartite matching값들의 합이 최소가 되는 $\sigma$(permutation)를 Hungarian algorithm을 이용해서 찾는게 목표이다. 해당 match에서는 class의 일치와 boxe의 일치 모두 고려한다고 한다. $y_i$는 $(c_i,b_i)$로 $c_i$는 class, $b_i$는 bbox에 대한 4개의 숫자로 이루어진 vector정보로 구성되어있다.
\[\sigma = \underset{\sigma \in S_N}{\arg\min} \sum_{i}^{N} \mathcal{L}_{\text{match}}(y_i, \hat{y}_{\sigma(i)})\]이렇게 되었을 때 $\hat y_{\sigma(i)}$는 $\hat p_{\sigma_(i)}(c_i)$로 표현이 되는데, 이는 $\sigma_(i)$일 때 $c_i$일 확률을 의미하게 된다. 그렇게 $\mathcal{L}{\text{match}}(y_i, \hat y{\sigma_(i)})$는 아래와 같은 식으로 표현 될 수 있다. 왼쪽은 class 분류 손실, 오른쪽은 bbox 손실로 표현이 된다. 왼쪽식은 해당 정답 클래스 확률이 큰게 목표이니 커지면서 -가 붙어 loss가 작아지는 쪽이 되고, 오른쪽은 두 bbox가 같아서 0으로 수렴하게 되는게 목표가 되어 총 손실함수는 작아지는 쪽으로 표현이 된다.
\[-1_{\{\hat{c}_{i} \neq \emptyset\}} \, \hat{p}_{\sigma(i)}(c_{i}) + 1_{\{c_{i} \neq \emptyset\}} \, \mathcal{L}_{\text{box}}(b_{i}, \hat{b}_{\sigma(i)}).\]해당 부분이 기존의 Detector model들에서 사용된 match proposal, anchors를 맞추는 부분을 대체 한다고 볼 수 있다. 가장 큰 차이점은 direct set prediction을 이용하기 때문에 중복 제거가 되며 one-to-one matching이 된다는 부분이다.
위에서 구한 표현법을 이용해서 Hungarian algorithm의 loss를 구하게 되면 아래와 같은 수식으로 정의된다. 여기서 $\hat \sigma$는 처음에 구했던 최적의 $\sigma$이다. 만약 $c_i = \varnothing$인 경우 가중치를 10배 낮춰 클래스 불균형을 해소한다고 한다. 그렇게 $\varnothing$ matching cost는 예측에 의존하지 않고 cost는 일정하다.
\[\mathcal{L}_{\text{Hungarian}}(y, \hat{y}) = \sum_{i=1}^{N} \left( -\log \hat{p}_{\hat \sigma(i)}(c_{i}) + 1_{\{c_{i} \neq \emptyset\}} \, \mathcal{L}_{\text{box}}(b_{i}, \hat{b}_{\hat \sigma(i)}) \right),\]Bounding box loss.
일반적으로 많이 사용되는 $\ell_1$ loss는 상대적인 오차가 비슷하더라도 작은 박스와 큰 박스에 대해 서로 다른 갖는 문제점이 있엇기 때문에 이를 완화하기 위해 스케일 불변인 $\ell_1$ loss와 $\mathcal{L}_\text{iou}$를 결합하여 bounding box loss가 표현이 된다.
\[\lambda_{\text{iou}} \, \mathcal{L}_{\text{iou}}(b_{i}, \hat{b}_{\sigma(i)}) + \lambda_{\text{L1}} \, \|b_{i} - \hat{b}_{\sigma(i)}\|_{1}, \quad \text{where } \lambda_{\text{iou}}, \lambda_{\text{L1}} \in \mathbb{R}\]3.2 DETR architecture
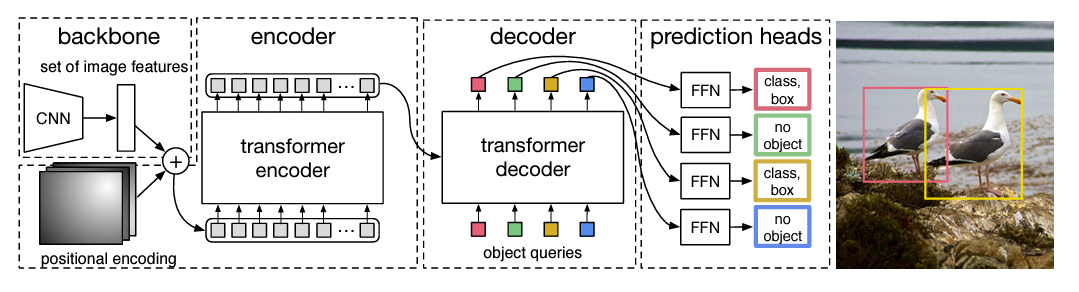DETR은 크게 CNN, encoder-decoder Transformer, feed forward network (FFN)로 simple하게 구성되어 있다.
Backbone.
입력으로 들어오는 image $x_{\text{img}} \in \mathbb{R}^{3 \times H_0 \times W_0}$를 compact feature representation으로 표현하기 위해 CNN backbone에 들어가게 되고 $C=2048$, $H,W = \frac{H_0}{32}, \frac{W_0}{32}$로 정의된 $\mathbb{R}^{C \times H \times W}$차원을 가진 형태로 출력이 된다.
Transformer encoder.
먼저 channel dimension을 줄이기 위해 1x1 convolution을 이용하여 $\mathbb{R}^{d \times H \times W}$ 차원으로 줄여주고 이를 $z_0$라고 표현한다. 또 sequence 형태로 표현하기 위해 $d \times HW$형태로 표현해준다. encoder 구조는 Multi-Head Self-Attention과 FFN구조로 이루어져 있고 Transformer는 입력 시퀀스의 순서를 인식하지 못하는 순열 불변성(permutation-invariant)이므로 순서 정보를 보존하기 위해 positional encoding을 추가해준다.
Transformer decoder.
decoder는 기존의 transformer의 standard한 architecture를 따르며 $d$크기의 $N$개의 embedding으로 변환하는 Multi-Head Attention 구조를 가진다. 기존의 decoder 다른 부분은 N개의 object를 병렬적으로 decoding한다는 것이다.
decoder역시 permutation-invariant 특성을 가지므로 learned positinal encodings인 Object Query를 디코더의 입력으로 사용된다. 신기하게도 object query는 positinal encoding의 역할과 encoder의 출력값들에 대한 정보를 학습하는 query의 역할을 동시에 하고 있다. 그렇게 추가된 N개의 object query는 decoder의 단계를 거쳐 class와 bbox를 최종 예측할 수 있게 된다.
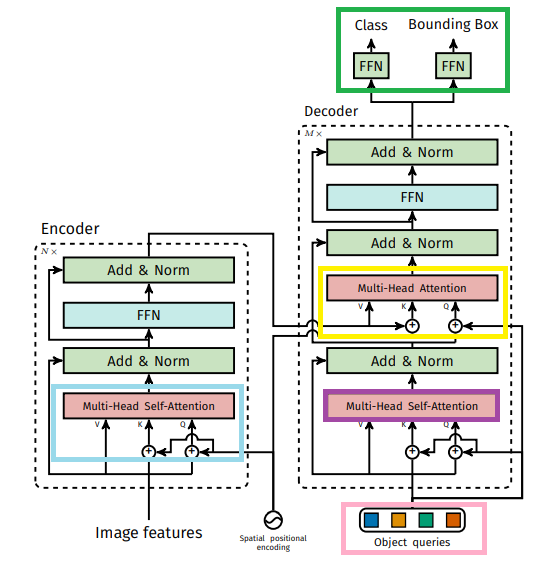
Prediction feed-forward network (FFNs).
마지막 FFN은 ReLU함수를 사용하는 3-layer perceptron과 linear projection으로 구성되어 있다. Bounding Box는 중심좌표와 h,w로 구성되어있고, Class는 softmax function을 통해 예측을 한다. $\varnothing$로 검출이 되기도 하는데 이는 background class로 이해시킨다고 한다.
Auxiliary decoding losses.
decoder label뒤에 예측 FFN과 Hungarian loss를 추가하여 보조 loss로 사용하면 학습에 도움된다고 한다.
4. Experiments
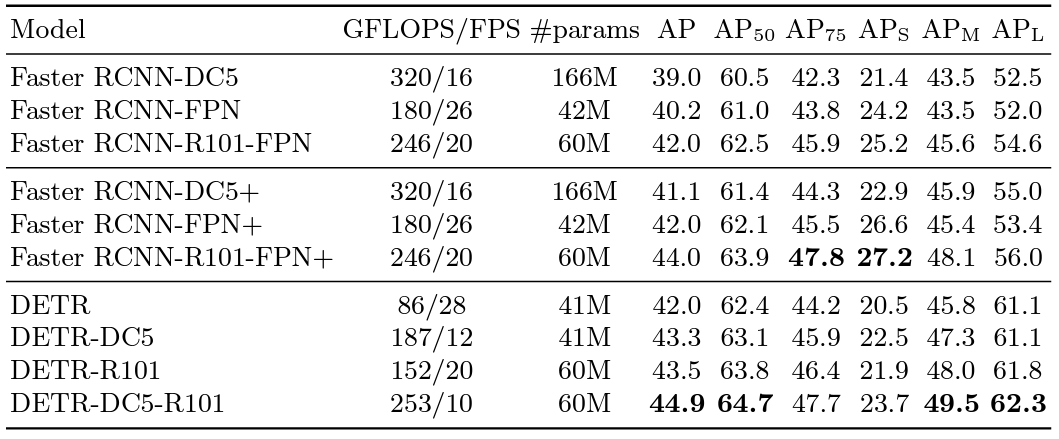
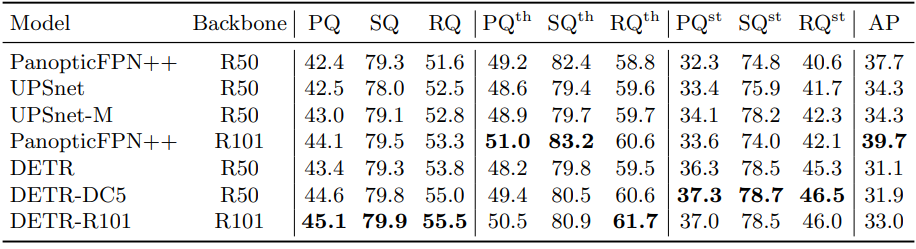
4.1 Comparison with Faster R-CNN
기존의 SOTA 모델이였던 Faster R-CNN과 성능 비교를 보여주는 정량적 지표이다.
4.2 Ablations
row에서 encoder layers에 따른 성능 변화를 확인할 수 있다.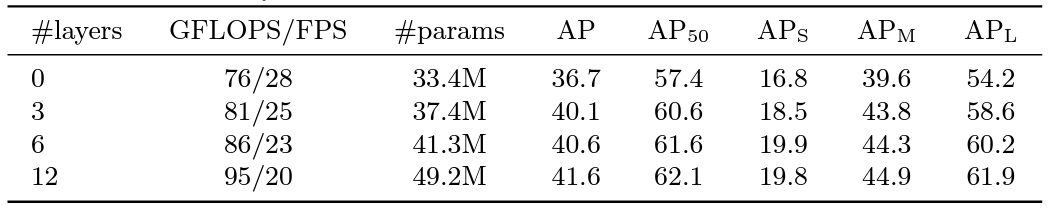 
마지막 encoder layer에서의 attention maps를 visualize한 모습이다. 
다음은 rare classes의 distribution generalization을 보여주는 모습이다.
출력 결과물과 decoder의 attention maps를 visualize한 모습이다.
4.3 Analysis
Decoder output slot analysis
Generalization to unseen numbers of instances.
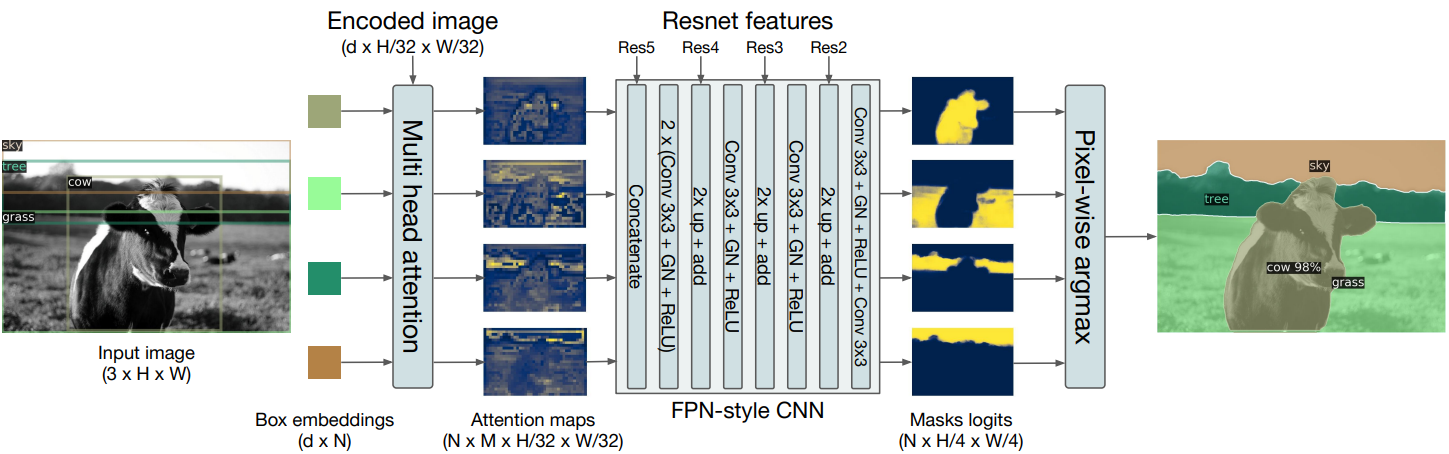
4.4 DETR for panoptic segmentation
DETR의 decoder outputs단에 adding mask를 통하여 panoptic segmentation task를 수행하는 것을 도식화로 보여준다.
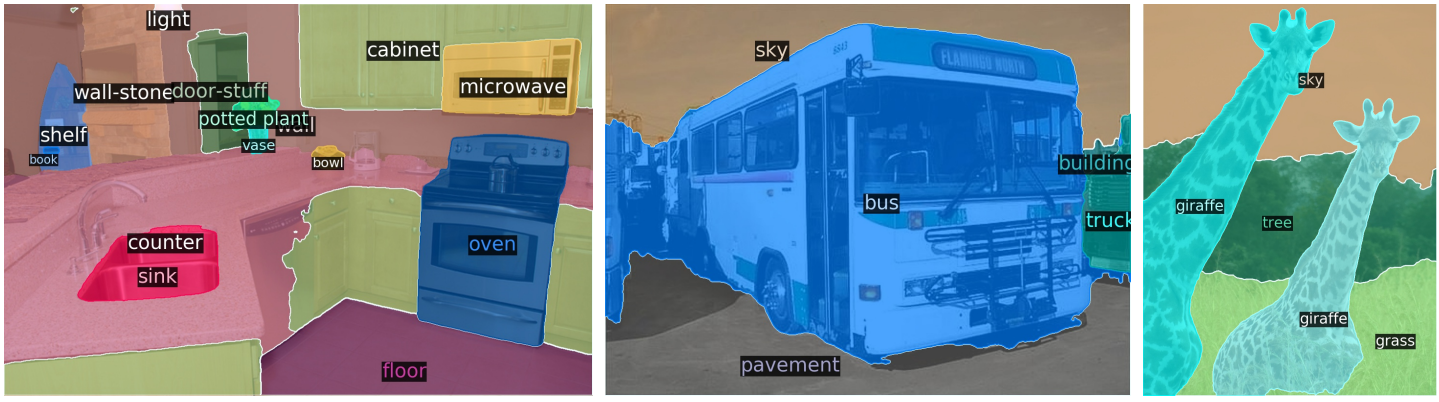
5. Conclusion
DETR(Detection Transformer)은 새로운 객체 탐지 접근 방식으로, Transformer를 활용하여 객체 탐지 문제를 End-to-End로 해결하는 모델이다. 전통적인 Detection과 달리 anchor와 비최대 억제(non-maximum suppression) 같은 후처리 과정을 필요로 하지 않으며, transformer 구조를 이용하여 detection task를 성공적으로 수행한다.
Reference.
Enjoy Reading This Article?
Here are some more articles you might like to read next: