[Papers] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (ECCV 2020)
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
[Paper] [Github] [Demo]
Title: NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
Journal name & Publication year: ECCV 2020
First and Last Authors: Ben Mildenhall
First Affiliations: UC Berkeley, Google Research, UC San Diego
Abstract & Introduction
NeRF는 Novel View Synthesis(NVS) 계열의 기술이며 입력으로 들어오는 이미지들을 통해 특정 위치에서 해당 물체를 바라보는 synthetic image를 생성하는 기술이다. “for View Synthesis”라는 표현을 새로운 시점의 생성이라는 뜻으로 이해할 수 있다.
한마디로 지금까지 관측한 이미지들로부터 관측하지 못한 시점에서의 image를 생성하는 기술이다.

NeRF의 PipeLine은 크게 2단계의 과정으로 나눌 수 있다.
- Neural Network(MLP)를 통한 3D 공간 특징 추출
- Volume Rendering을 통한 2D 이미지 생성
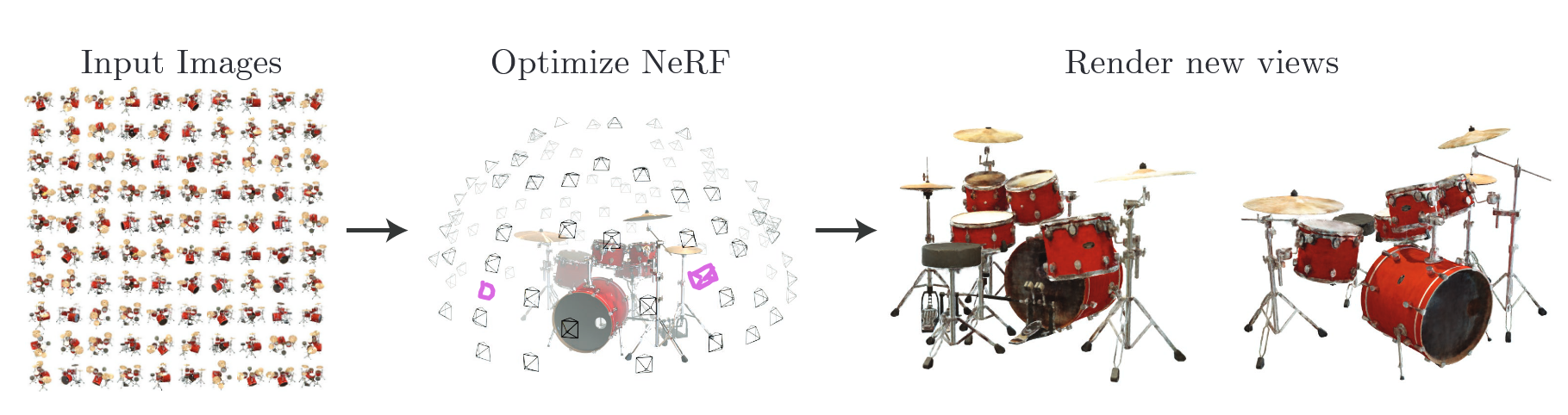
이 외에도 High-Resolution과 High-Frequency를 위한 Positional Encoding, Sampling 등에 대한 부분은 Optimizing 부분에서 확인해볼 예정이다.
Neural Radiance Field Scene Representation
가장 먼저 살펴볼 부분은 밀도 및 색상을 예측 하는 MLP부분이다. 입력으로는 3D 좌표인 $x = (x, y, z)$와 시점을 나타내는 $d(θ, φ)$ 값이 들어가서 해당 좌표의 RGB 값 $c = (R,G,B)$와 density 값인 $σ$가 출력이 된다.
\[FΘ : (x, d) → (c, σ) \quad{} FΘ : (x,y,z,θ, φ) → (R,G,B,σ)\]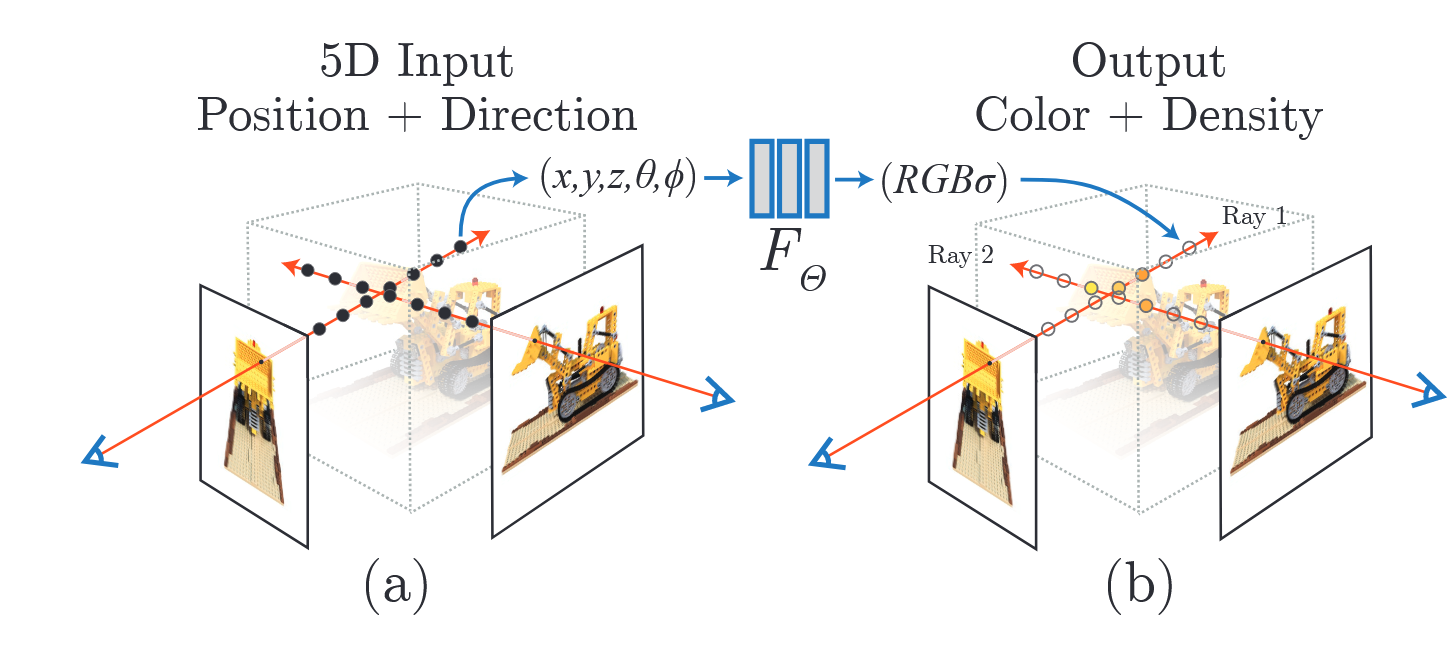
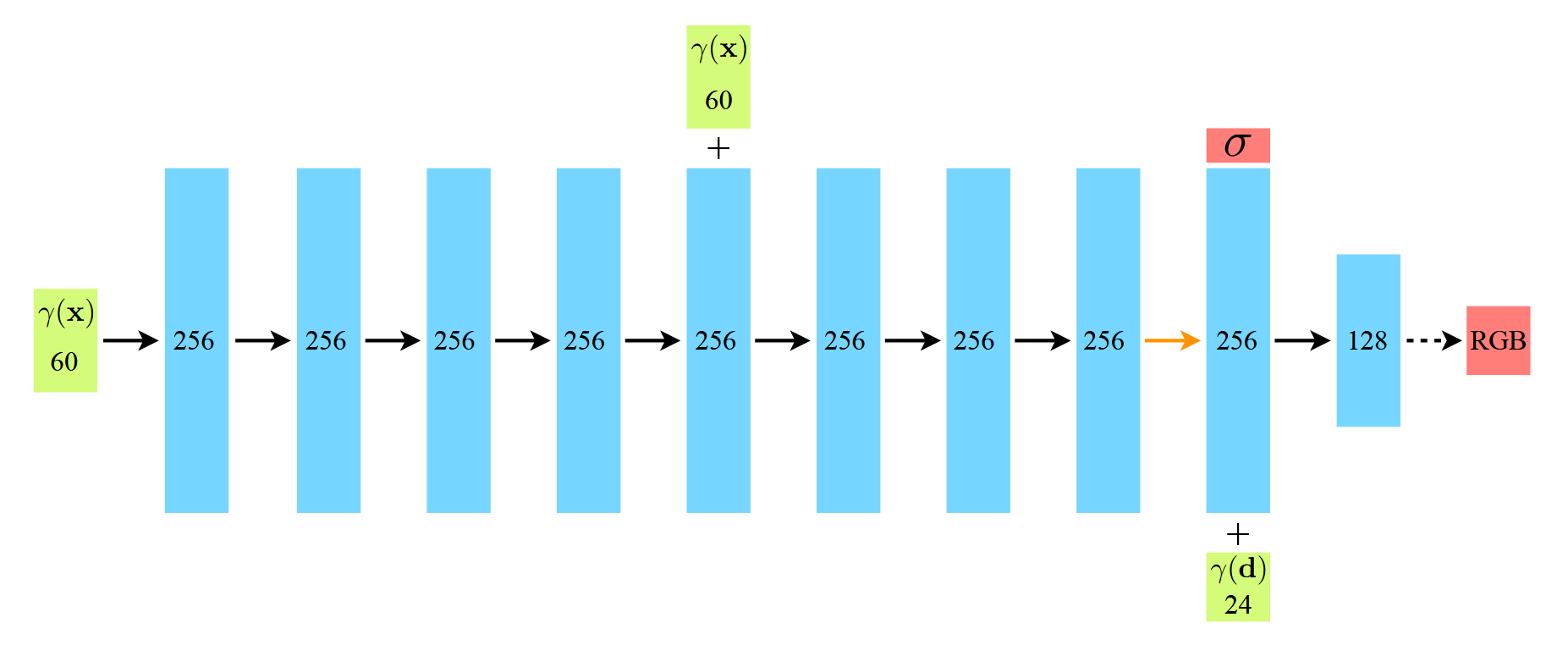
MLP는 아래와 같이 구성되어 있다. 검은색 화살표는 Linear + ReLU을 거치게 되고 노란색 화살표는 Linear로만 이루어져있으며, 마지막 점선 화살표는 Linear + Sigmoid로 이루어져 있다.중간중간의 + 는 Concatenate를 의미한다.
처음으로 들어오는 입력값 position x가 3차원이 아닌 60차원으로 들어오게 된다. 이는 Positional Encoding과정을 거치기 때문인데 이는 쉽게 말해서 3차원 값으로는 표현하지 못하는 영역을 60차원으로 표현하여 디테일을 높여주기 위함이다.
Positional Encoding의 목적
원인 : 일반적으로, NeRF의 MLP는 10개의 층과 뉴런으로 이루어진 단순한 구조이다. 이는 저주파(low-frequency) 정보를 학습하는 데 적합하며, 고주파(high-frequency) 정보를 학습하는 데 한계가 있다.
- 저주파 정보: 부드럽고 점진적인 변화 (배경 색상)
- 고주파 정보: 날카로운 경계나 세부적인 구조 (물체의 윤곽, 텍스쳐 등)
따라서, 단순히 3D 좌표를 입력하면 고주파 정보를 제대로 학습할 수 없고, 결과적으로 부드럽고 디테일이 부족한 장면을 생성하게 된다.
그럼 왜 60차원인가? 3D 좌표의 각 차원을 2L개의 주파수 성분으로 확장(L=10)하며, 이는 총 $3 \times 2L = 60$이 된다.

그리고 중간 5번째 layer에서 입력으로 들어온 60차원의 좌표값과 똑같은 값이 concatenate되는 부분은 일종의 skip connection의 역할로 모델 학습의 안정성과 효율성을 높이기 위함이다.
8번째 레이어에서 밀도(density) 값이 출력되는데, 이는 해당 좌표를 바라보는 direction 값과는 무관하다는 것을 알 수 있다. 밀도란 개념은 바라보는 시점(viewpoint)에 따라 달라지는 값이 아니라, 특정 좌표 그 자체에서 고정되는 값이기 때문이다. 따라서 NeRF의 MLP 내부에서 밀도 값은 Positional Encoding을 통해 확장된 좌표 값만을 입력으로 받아 계산된다.
이후, direction 값 $d$가 concatenate되어 MLP는 해당 좌표와 방향 정보를 조합해 픽셀의 $(R,G,B)$ 값을 출력하게 된다. 이는 색상 값이 시점에 따라 달라지는 view-dependent 특성을 학습하기 위해 설계된 과정이다. 예를 들어 빛 반사나 굴절은 시점에 따라 달라질 수 있기 때문이다.

밀도(density)와 direction의 관계
- 밀도는 특정 좌표가 얼마나 “물질”이 있는지 나타내는 값으로, 시점(view)에 독립적이다. 이는 density field가 3D 공간의 고유한 물리적 특성을 나타낸다고 할 수 있다.
- 반면, 색상 정보는 바라보는 방향에 따라 빛의 반사나 굴절이 달라 질 수 있기 때문에 view-dependent한 특성을 가지게 된다.
오케이 알겠는데 그럼 왜 이렇게 설계 했을까 ?
- 이는 view-independent한 정보와 view-dependent한 정보를 분리하여 모델이 더 효율적으로 학습할 수 있도록 설계했기 때문이다. 즉, 밀도와 색상 예측 과정을 하나의 MLP내부에서 분리하여 보다 정교한 3D 표현을 학습할 수 있게 설계 한 것이다.
Lambertian effects
- 논문에서 나오는 표현으로 람베르트 반사라는 용어이다. 이는 관찰자가 바라보는 각도와 관계없이 같은 겉보기 밝기를 갖는 성질을 의미한다.
- 하지만 NeRF는 direction값을 input으로 사용하기 때문에 각도에 따라 휘도가 달라지는 non-Labertian effects성질을 갖게 되는 것이다.
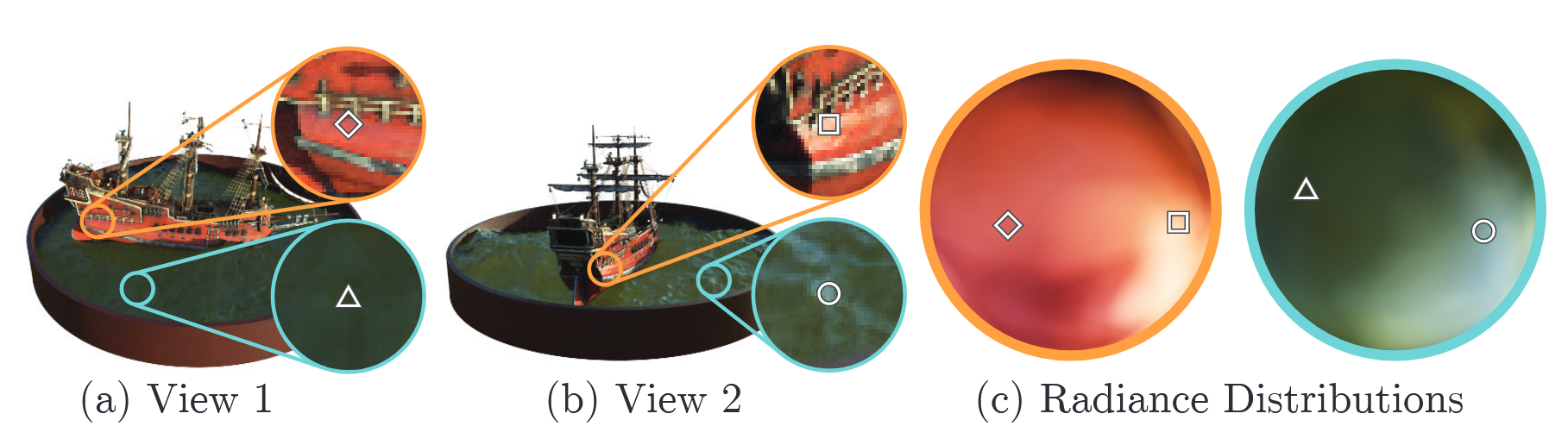
Volume Rendering with Radiance Fields
5D를 통해 나온 $c$(color)와 $\sigma$(density)를 통해서 2D Image를 생성하기 위해 Computer Graphics의 고전적인 방법론인 volume rendering을 사용한다.
수식을 간단하게 살펴보자면 결과 값인 $C(\mathbf{r})$은 하나의 ray(pixel)에서 기대할 수 있는 Color값(expected color)을 의미하게 된다.
\[C(\mathbf{r}) = \int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) c(\mathbf{r}(t), \mathbf{d}) \, dt, \quad \text{where} \quad T(t) = \exp \left( - \int_{t_n}^t \sigma(\mathbf{r}(s)) \, ds \right).\]
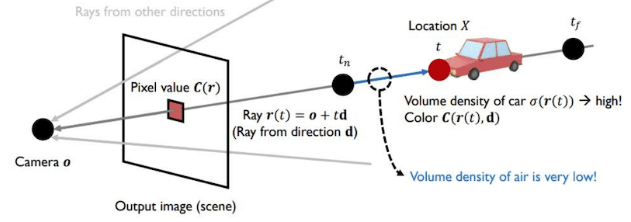
- $t$: t는 ray의 깊이(depth)를 의미하는 parameter로, 카메라에서 시작된 광선이 3D 공간에서 특정 지점에 도달하기까지의 거리(depth)를 의미한다. $t_n$은 광선이 시작되는 지점, $t_f$는 광선이 끝나는 지점을 의미한다.
- $\sigma(\mathbf{r}(t))$: 해당 시점에서의 density값으로 볼 수 있으며 값이 커질수록 Weight가 커지게 된다.
- $T(t)$: Transmittance(빛의 투과도)를 의미하며 수식적으로 보았을 때 density값이 커질 수록 작아진다는 것을 알 수 있다. 이를 해석해보자면 우리가 보려고 하는 물체 앞에 밀도를 가지는 물체가 있을 때 우리가 보고자 하는 물체가 가려지게 되는 것을 수식적으로 표현했다고 볼 수 있다. pixel은 해당 값이 클 수록 투명하고 작을수록 불투명하게 된다.
- $c(\mathbf r(t),d)$: 해당 ray와 시점에 대한 물체의 색을 나타내는 부분이다.
정리하면, 한 픽셀의 색상은 광선(ray)의 모든 지점에서 (전달된 투과도) × (밀도) × (색상) 을 누적하여 적분한 값과 같다. 이 적분은 광선 상의 작은 간격($dt$)에 대해 수행된다.
continuous(연속적인) 한 적분식을 실제로 프로그래밍에 사용할 수 있게 하기 위해 discrete(이산적인)하게 변환해야 한다. 그래서 수치적 방법으로 아래와 같이 근사하게 된다. 여기서 사용되는게 Stratified sampling으로, 고정된 간격의 샘플링을 하는 것이 아니라 각 구간에 대해서 무작위 샘플링을 하게 되어 적분의 정확성을 향상 시키게 되었다고 설명한다. 결론적으로 무작위 샘플링을 통해 적분을 근사하여 연속적인 장면을 표현할 수 있는 것이다.
\[t_i \sim \mathcal{U} \left[ t_n + \frac{i-1}{N}(t_f - t_n), \, t_n + \frac{i}{N}(t_f - t_n) \right]\]그렇게 위에서 샘플링된 $c_i$와 $\sigma_i$값들을 기반으로 $\hat{C}$를 계산하게 된다.
\[\hat{C}(\mathbf{r}) = \sum_{i=1}^N T_i \left(1 - \exp(-\sigma_i \delta_i)\right) c_i, \quad \text{where} \quad T_i = \exp\left(-\sum_{j=1}^{i-1} \sigma_j \delta_j\right)\]
- $T_i$: 남아있는 빛의 양 (투과도)
- $(1-\exp(\sigma_i\delta_i))$: 해당 지점에서 흡수된 빛의 양 (불투명도)
- $c_i$: 해당 지점의 색상
- $\hat{C}$: 각 샘플링 지점의 색상 값을 가중합한 결과로 최종 픽셀 색상
Optimizing a Neural Radiance Field
Positional encoding
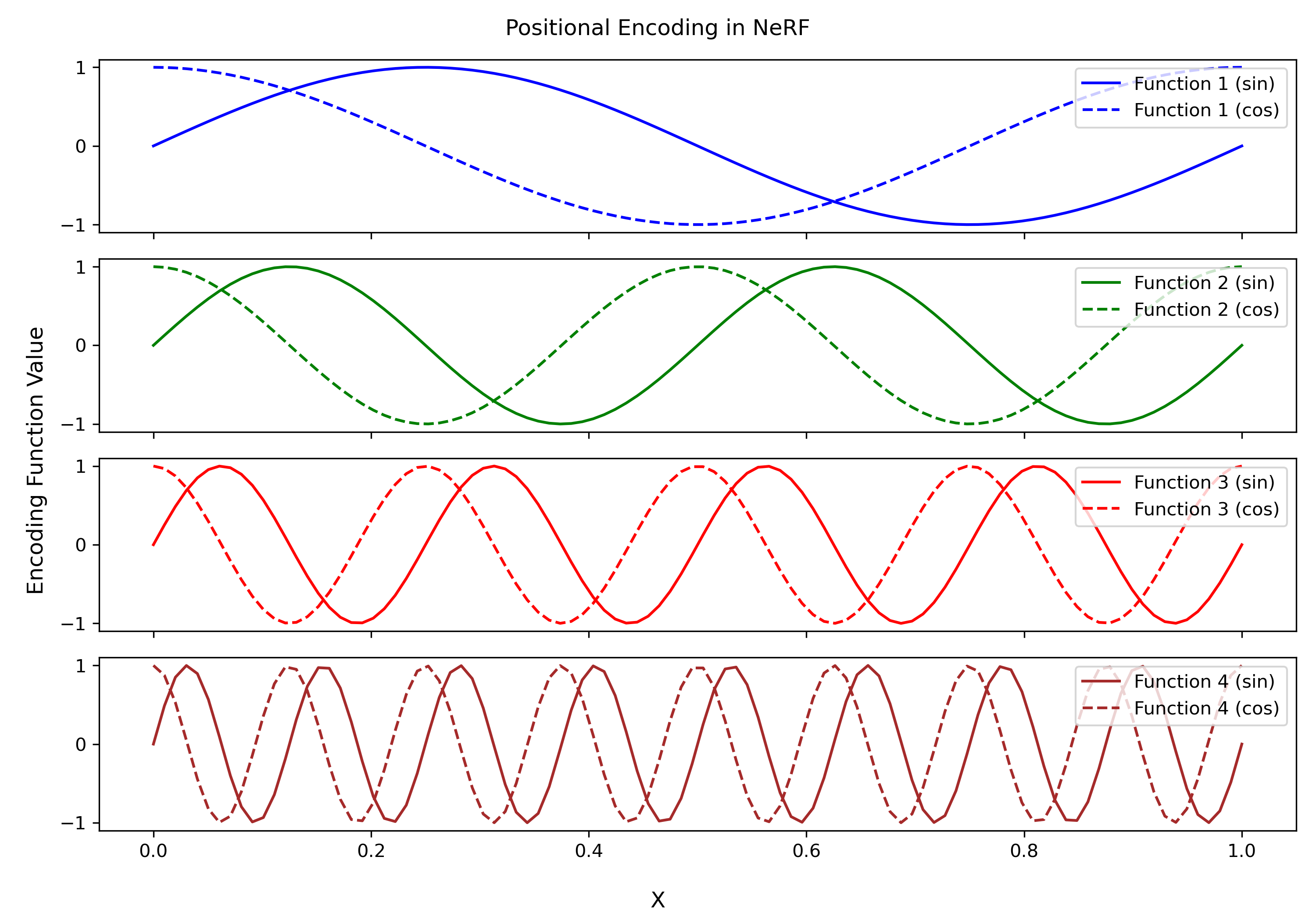
이전에 MLP 부분에서 3차원 좌표를 60차원 입력으로 변환할 때 사용되는 Positional Encoding 기법에 대한 설명이다. 다시 한번 복기하자면 더 높은 고차원으로 표현을 하여 고주파 정보 즉, 물체의 윤곽과 텍스쳐에 대한 detail 정보들을 출력할 수 있게 된다.
\[\gamma(p) = \left( \sin(2^0 \pi p), \cos(2^0 \pi p), \cdots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p) \right).\]
- 저주파 정보: 부드럽고 점진적인 변화 (배경 색상)
- 고주파 정보: 날카로운 경계나 세부적인 구조 (물체의 윤곽, 텍스쳐 등)
Hierarchical volume sampling
기존의 방식들은 빈 공간(free space) 이나 가려진 영역(occluded regions)과 같이 렌더링에 기여하지 않는 부분도 반복적으로 샘플링하였기 때문에 매우 비효율적 이었다.
NeRF의 Hierarchical Sampling은 장면의 중요 영역에 샘플링을 집중하여 렌더링 효율과 품질을 높이는 전략이다. Coarse Network와 Fine Network를 동시에 최적화 하게 된다. Coarse Network에서는 전체적인 이미지, Fine Network에서는 중요한 영역에 대해 집중하게 된다.
\[\hat{C}_c(\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i, \quad w_i = T_i \left(1 - \exp(-\sigma_i \delta_i) \right).\]
- Coarse Sampling: Stratified Sampling을 사용해 고르게 샘플링.
- PDF 생성: Coarse Network의 출력을 바탕으로 확률 밀도 함수(PDF)를 생성.
- Fine Sampling: PDF를 기반으로 Inverse Transform Samplingdmf 사용하여 중요한 영역에서 추가 샘플링.
- 최종 렌더링: Coarse와 Fine 샘플을 결합하여 최종 이미지를 생성.
이 과정은 샘플링 효율성을 극대화하고, 빈 공간에 낭비되는 계산을 줄이는 동시에 중요한 영역의 디테일을 더 잘 포착하도록 설계하였다
Loss
그렇게 Coarse Network와 Fine Network를 통해 나온 output을 통해 실제 Ground Truth와 L2 Norm을 이용하여 Loss를 간단하게 구성된다.
\[L = \sum_{r \in R} \left[ \| \hat{C}_c(r) - C(r) \|_2^2 + \| \hat{C}_f(r) - C(r) \|_2^2 \right]\]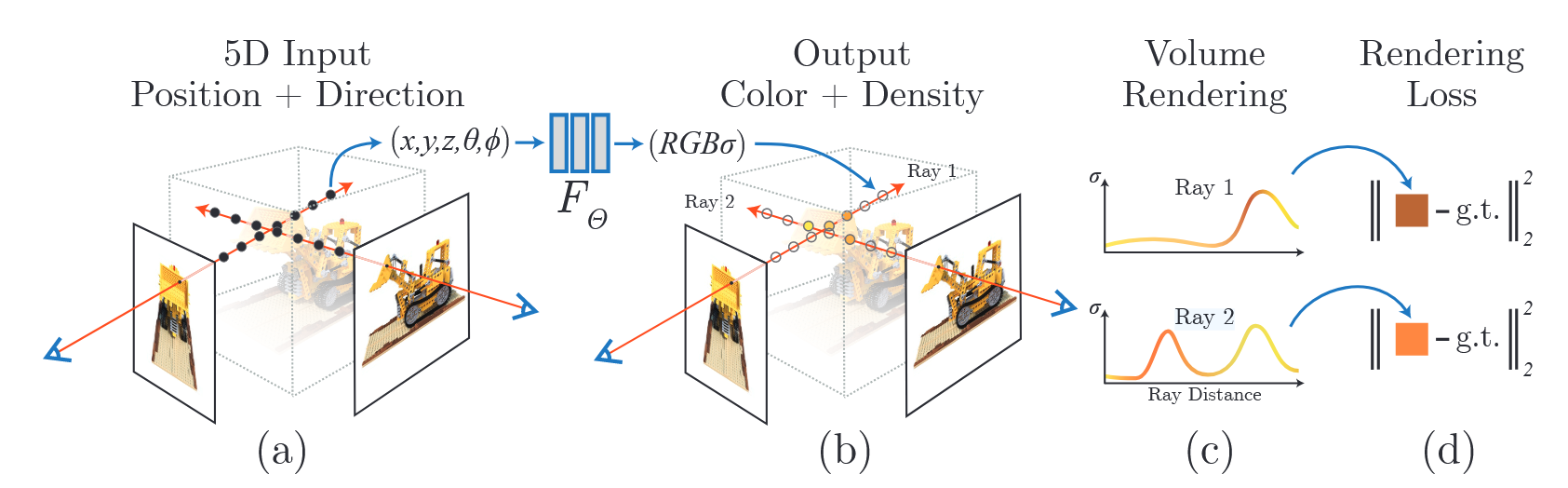
Results



Reference.
https://arxiv.org/abs/2003.08934
https://github.com/bmild/nerf
https://csm-kr.tistory.com/64
https://jaehoon-daddy.tistory.com/26
https://www.youtube.com/watch?v=Mk0y1L8TvKE
https://an067.pages.mi.hdm-stuttgart.de/or-jupyterbook/05_NeRF_improvements/05_NeRF_improvements
Enjoy Reading This Article?
Here are some more articles you might like to read next: